【信息学竞赛-算法竞赛 讲解】Tarjan缩点

一、关于Tarjan算法

Tarjan 算法是基于对图深度优先搜索的算法，每个强连通分量（SCC）为搜索树中的一棵子树。搜索时，把当前搜索树中未处理的节点加入一个堆栈，回溯时可以判断栈顶到栈中的节点是否为一个强连通分量。

主要用于解决缩点问题。缩点就是将图中的一个环经过处理后视作一个点。从而将一个有向有环图转换为一个有向无环图（DAG）。（前提：有向图，环->点）所以经常用于解决非简单路径问题。

SCC--有向图而言，一个极大环就是一个强连通分量。有向图至少两点成环。

二、Tarjan思路

1.四种有用的边（重点记住返祖边和横叉边）

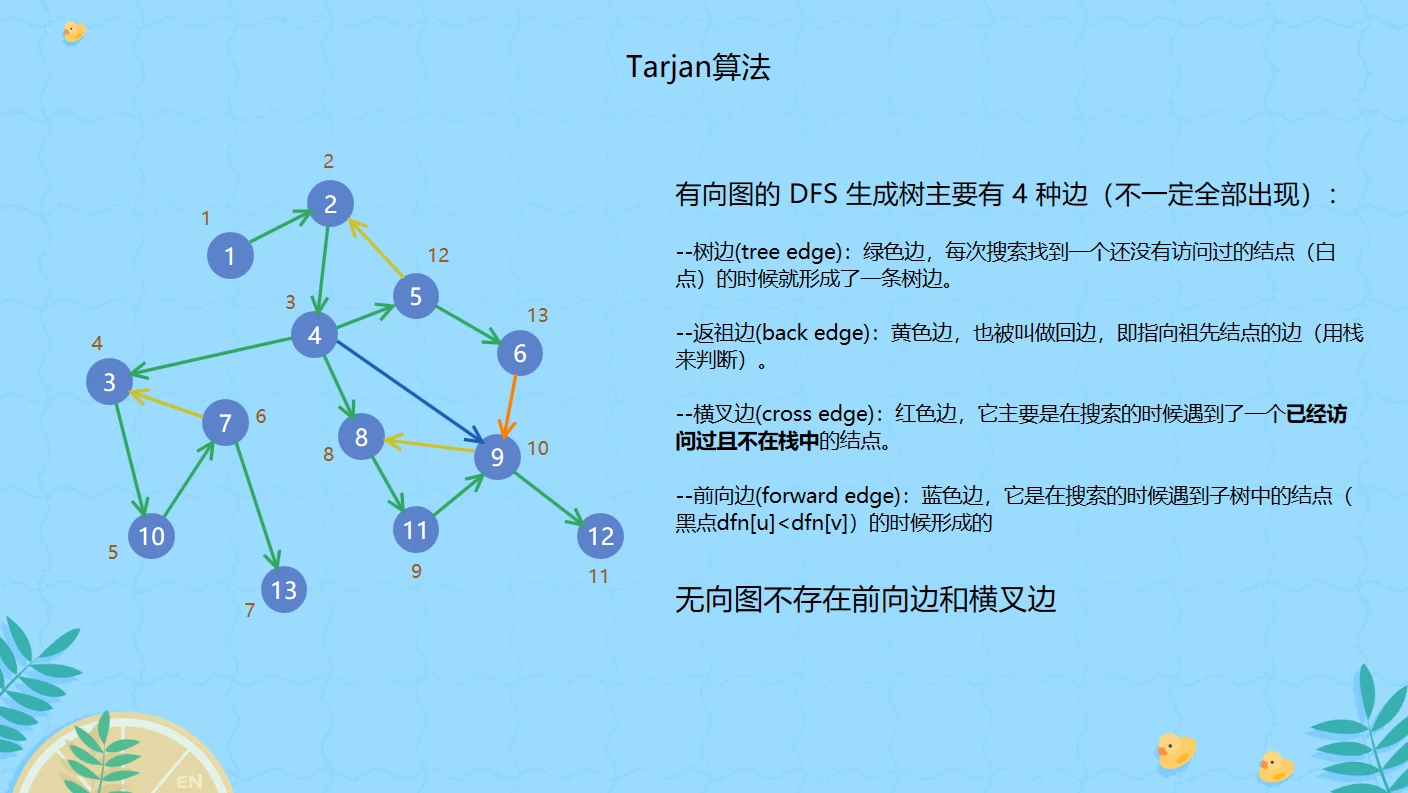
2.算法思路

Tarjan基于对图的深度优先搜索，并对每个节点引入两个值：

--dfn[u]：节点 u 的时间戳，记录点 u 是 DFS 过程中第几个访问的节点。

--low[u]：记录节点u或u的子树不经过搜索树上的边(树边)能够到达的时间戳最小的节点。（必须理解透这个含义）

--初始时，dfn[u]==low[u]。

--对 u 的邻接边 <u,v> 若在搜索树，即边 <u,v> 是树枝边（找到一个新的点），则更新low[u] = min(low[u], low[v])；

--若 <u,v> 是返祖边（v是一个访问过的点），则更新：low[u] = min(low[u], dfn[v])；

3.逻辑细化

在有向图中，我们经常需要把一个SCC缩成一个点（Tarjan本质），然后生成一个有向无环图(DAG)，或把一个无向图缩点后变成一棵树，然后可以有很多优秀的性质进行解决。

算法实现：

1. 从图的某一点 u 开始，对图进行 DFS(u)，点维护 dfn[u] 值和 low[u] 值；
2. DFS 时先将 u 压入栈中，然后遍历邻接边，邻接边定点为 v；
3. 如果<u,v> 为树边，DFS(v)，回溯时更新：low[u] = min(low[u], low[v])；
4. 如果<u,v> 为返祖边，更新：low[u] = min(low[u], dfn[v])；
5. 节点 u 变黑，即其所有子树访问结束时，若 dfn[u]==low[u] 时，此时栈顶节点到节点 u，为一个 SCC。

三、真题演练

1.洛谷T564912 无向图缩点

• 题目大意：给出一幅n个点，m条边的无向图，求其中点数大于1的边双联通分量个数。
• 注意：无向图两点不能成环
• 题目思路：
  • 函数 Tarjan： 这是算法的核心部分，用于找到图中的割点和连通分量：
    • 使用深度优先搜索（DFS）遍历图。
    • 对于每个节点 u，更新其 low 和 dfn 值（初始为low[u]=dfn[u]=++time;）。
    • 遍历当前节点的所有邻接节点 v：
      • 如果 v 是 u 的父节点，则跳过。
      • 如果 v 还未被访问，递归调用 Tarjan，并更新 low[u]。
      • 如果 v 已经被访问，更新 low[u] 为 dfn[v]。
    • 当发现一个连通分量的根节点时（即 low[u] == dfn[u]），通过栈 st 找到该连通分量中的所有节点，并计算其大小。
  • 结果计算：遍历一遍size数组，记录其中大于1的个数
• AC代码：

#include <cstdio>
#include <algorithm>
using namespace std;

const int maxn = 2e4 + 5;
const int maxm = 2e5 + 5;

struct Edge {
	int u, v, next;
} e[maxm * 2];

int head[maxn], tot = 0;
void insert(int u, int v) {
	e[++tot] = {u, v, head[u]}; // 创建新边并更新邻接表
	head[u] = tot; // 更新头指针
}

int n, m;
void input() {
	scanf("%d %d", &n, &m);
	for (int i = 1; i <= m; ++i) {
		int u, v;
		scanf("%d %d", &u, &v); // 读取每条边
		insert(u, v); // 插入边 u -> v
		insert(v, u); // 插入边 v -> u (无向图)
	}
}

// Tarjan 算法相关变量
int low[maxn], dfn[maxn], cnt = 0, time = 0, size[maxn];
int st[maxn], top = 0; // 栈用于存储当前路径上的节点

// Tarjan 算法的实现
void Tarjan(int u, int fa) {
	low[u] = dfn[u] = ++time; // 初始化 low 和 dfn 值
	st[++top] = u; // 将当前节点压入栈
	for (int i = head[u]; i; i = e[i].next) { // 遍历邻接节点
		int v = e[i].v; // 当前邻接节点
		if (v == fa) { // 如果是父节点，跳过（避免死循环）
			continue;
		}
		if (dfn[v] == 0) { // 如果 v 未被访问
			Tarjan(v, u); // 递归访问
			low[u] = min(low[u], low[v]); // 更新 low[u]
		} else {
			low[u] = min(low[u], dfn[v]); // 更新 low[u]
		}
	}

	// 判断是否为强连通分量的根节点
	if (low[u] == dfn[u]) {
		++cnt; // 找到一个连通分量
		while (st[top] != u) { // 处理当前连通分量，缩点
			--top; // 弹出栈顶元素
			++size[cnt]; // 更新连通分量大小
		}
		--top; // 弹出当前根节点
		++size[cnt]; // 根节点本身也要计入大小
	}
}

int main() {
	input(); // 输入图的信息
	for (int i = 1; i <= n; ++i) { // 遍历所有节点
		if (dfn[i] == 0) { // 如果节点未被访问
			Tarjan(i, 0); // 从该节点开始 DFS
		}
	}

	int ans = 0;
	for (int i = 1; i <= cnt; ++i) { // 遍历所有连通分量的大小
		if (size[i] > 1) { // 如果连通分量的大小大于 1
			++ans; // 统计有效连通分量
		}
	}
	printf("%d", ans);
	return 0;
}